Contents

4. Numpy

3장에서는 파이썬의 대표 데이터 분석/처리 라이브러리라고 할 수 있는 Pandas에 대해 알아보았습니다. 4장에서는 파이썬의 대표 선형대수 라이브러리인 Numpy에 대해 알아보겠습니다.

  • 그림 4-1 Numpy 로고(출처)

Numpy는 연구하시는 분들 뿐만 아니라 현장에서 데이터 사이언스 하시는 분들과 더불어 수치해석 쪽을 하시는 분들도 주로 사용하는 라이브러리 입니다.

2005년에 Travis Oliphant가 서로 다른 장단점이 있던 Numeric 라이브러리와 Numarray 라이브러리를 결합해서 Numpy v1.0를 출시 했습니다. 그 때 부터 Numpy에서 고성능의 벡터/행렬 연산 및 바이너리 데이터 타입을 지원하기 시작했습니다. 2005년 전에는 수치해석이나 선형대수를 하기 위해 대부분 Matlab과 같은 유료 소프트웨어를 사용했었습니다. 하지만 Numpy와 Scipy 같은 라이브러리가 나오면서 최근들어 Matlab보다 파이썬을 활용하는 경우가 많아졌습니다.

4.1 Numpy 설치

Numpy 설치는 3.1절에 나온 Pandas 설치 방법과 유사합니다. Anaconda Navigator 사용자는 Environments 탭에 가서 Numpy를 설치하고자 하는 가상환경을 선택 후 Numpy를 체크하면 설치가 됩니다.

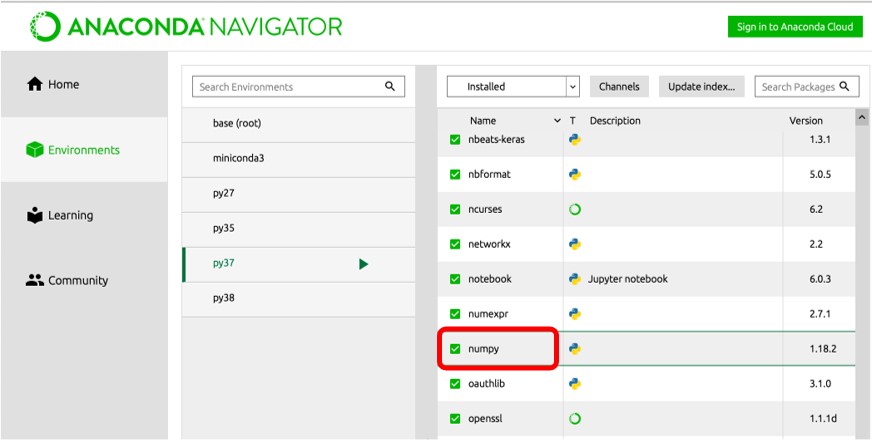
  • 그림 4-2 Anaconda Navigator에서 Numpy 설치(출처)

터미널을 사용하는 분들은 conda activate [가상환경 이름] 명령어를 통해 가상환경을 실행하고 pip install numpy명령어를 통해 numpy를 설치합니다. 이미 Numpy가 설치 되어 있을 경우 pip install -U numpy명령어를 통해 최신 버전으로 업그레이드 할 수 있습니다.

4.2 Numpy 기초

Numpy에서 가장 기본에 되는 데이터 타입은 ndarray 이며 줄여서 array라고도 합니다. nd는 N-dimensional의 약자이며 ndarray는 임의의 차원의 array를 뜻합니다. ndarray 데이터 타입 보유한 속성들은 아래와 같습니다.

속성명

설명

ndarray.ndim

차원 개수

ndarray.shape

배열 크기

ndarray.size

배열의 원소 개수

ndarray.dtype

배열의 데이터 타입

ndarray.itemsize

원소의 바이트 크기

ndarray.data

배열의 데이터

  • 표 4-1 ndarray 데이터 타입이 지원하는 속성

각 속성에 대한 예제는 아래 그림 4-3에서 확인할 수 있습니다.

  • 그림 4-3 ndarray 속성 사용 예제(출처)

4.3 Numpy 인덱싱/연산

array는 인덱싱이 빠르며 벡터 또는 행렬 연산이 빠릅니다. 파이썬에서 제공하는 기본 데이터 타입인 리스트로 행렬을 만든다면 2행 3열의 원소를 접근하기 위해 b[2][3]처럼 대괄호를 총 4개를 사용해야 인덱싱이 가능합니다. 하지만 array에서는 b[2,3]처럼 간편하게 인덱싱이 가능합니다. 그림 4-4에서 array 인덱싱 예시를 확인할 수 있습니다.

  • 그림 4-4 array 인덱싱 예제(출처)

또한 array에서는 특정 범위를 지정해서 인덱싱이 가능합니다. b[0:5, 1]명령어는 1번째 열에 있는 0부터 4번째 행의 원소를 반환합니다. b[:, 1]명령어는 1번째 열에 있는 모든 행의 원소를 반환합니다.

또한 조건문을 통해서 인덱싱이 가능합니다. a 행렬 내에 존재하는 원소 중 4보다 큰 원소들만 보고 싶다면 먼저 a > 4 조건문을 b에 저장한 후, 조건문이 반환한 True, False로 이뤄진 array로 a를 인덱싱할 수 있습니다.

  • 그림 4-5 array 인덱싱 예제(출처)

array간의 사칙연산도 지원 됩니다. 크기가 같은 두 개의 array간 사칙연산을 실시하면 element-wise한 연산이 실행 됩니다. 또한 제곱 연산이나 기타 연산도 element-wise하게 적용 됩니다. 아래 그림을 통해 element-wise한 연산의 예시를 확인할 수 있습니다.

  • 그림 4-6 element-wise 연산 예제(출처)

array간 * 연산을 진행하면 element-wise한 곱셉이 실행됩니다. 행렬 곱셉을 구하기 위해선 @을 사용하거나 dot()함수를 사용해야 합니다. 아래 예시를 통해 확인할 수 있습니다.

  • 그림 4-7 행렬곱 연산 예제(출처)

4.4 Numpy 함수

아래 예제를 통해 Numpy가 제공하는 주요 함수들을 살펴보도록 하겠습니다.

  • 그림 4-8 random(), sum(), min(), max() 예제(출처)

그림 4-8에서 가장 첫번째로 등장하는 rg.random()함수는 난수를 생성합니다. 이때 rg에는 np.random.default_rng(1)가 저장돼있습니다. 그 다음에 나오는 sum(), min(), max()은 ndarray에서 제공하는 member function이며 총합, 최솟값, 최댓값을 산출해줍니다.

  • 그림 4-9 행/열 방향 연산(출처)

그림 4-9에서는 sum()과 min() 함수에 axis값을 주어 행 또는 열의 방향으로 연산을 하는 예시입니다. sum(axis=0)은 특정 열에 있는 모든 원소를 더해서 값을 반환하며 min(axis=1)는 특정 행에 있는 모든 원소 중 최솟값을 반환합니다. cumsum(axis=1)은 특정 행 방향으로 누적합을 구하는 명령어입니다.

이 외에도 numpy에서 제공하는 주요 함수들을 요약하면 아래와 같습니다.

함수

Column B

exp, log, expm1, log1p

지수함수 또는 로그함수를 사용해 숫자 변환

sqrt, square, abs

루트, 제곱, 절대값 산출

mean, median, var, std

평균, 중앙값, 분산, 표준편차 산출

sin, cos

sin, cos값 산출

corrcoef

상관계수 산출

concatenate, vstack, hstack

array 결합

reshape

array 크기 변경

  • 표 4-2 numpy에서 제공하는 주요 함수

Note

Numpy 공식 문서인 https://numpy.org/doc/stable/user/quickstart.html 에서 더 많은 예제들을 확인해 볼 수 있습니다.

4.5 선형회귀

선형회귀 모델은 여러 분야에서 가장 널리 쓰이는 모델 중 하나입니다. 선형회귀 모델은 종속변수와 독립변수 간의 관계를 선형 수식으로 표현합니다.

  • 그림 4-10 선형회귀 산식(출처)

  • 그림 4-11 주택 가격 예측을 위한 데이터(출처)

그림 4-10에 있는 식이 선형 회귀 모델의 예시입니다. 그림 4-11은 cs229에 나온 예제인데, 주택 가격을 예측하기 위해 평수와 방의 개수 정보가 같이 주어졌습니다. 주택 가격을 예측 하는 선형 회귀 모델을 구축하기 위해선 주택 가격을 종속변수로 두고 평수와 방의 개수를 독립변수로 두어 선형회귀 모델을 구축합니다.

  • 그림 4-12 손실함수 산식(출처)

해당 모델이 좋은 모델인지 아닌지 판별하기 위해서 손실함수를 사용합니다. 주택 가격 처럼 연속된 값을 예측하는 문제를 회귀문제라고 하는데 회귀문제에서 사용하는 대표적인 손실함수는 Mean Squared Error(평균제곱오차)입니다. MSE는 실제값과 예측값의 차이를 구한 뒤 제곱을 하고, 모든 오차의 제곱을 평균내어 구합니다. MSE가 작은 모델일 수록 성능이 좋은 모델이 되겠습니다.

선형회귀 모델 학습 시 목표는 손실함수가 최소가 되는 계수를 찾는 것입니다. 해당 계수를 찾기 위해 경사하강법을 사용하기도 하고 정규방정식(normal equation)을 사용하기도 합니다. 경사하강법은 선형회귀 모델 뿐만 아니라 이외의 알고리즘을 최적화 할 때도 사용하기 때문에 이번 장에서는 경사하강법에 대해 알아보겠습니다.

  • 그림 4-13 경사하강법(출처)

경사하강법을 통해 파라미터를 업데이트하는 방법은 손실함수를 특정 파라미터로 미분한 값에 임의의 상수를 곱해서 기존의 파라미터에 빼줌으로써 새로운 계수를 구합니다.

  • 그림 4-14 손실함수 미분 결과(출처)

  • 그림 4-15 선형회귀 모델의 경사하강법 산식(출처)

미분한 결과를 보면 모델 예측값에 실제값을 뺀 후 해당 피쳐를 곱해준 값과 같습니다. 그래서 각 샘플들을 입력할 때마다 경사하강법을 적용해서 지속적으로 계수를 업데이트 해줍니다. 이 때 알파값, 임의의 상수 값은 learning rate라고 하는데 해당 값이 너무 크면 업데이트가 되지 않기 때문에 일반적으로 작은 값을 사용합니다.

4.6 로지스틱회귀

앞서 선형회귀 모델은 종속변수가 연속형, 실수 였지만 로지스틱회귀 모델은 종속변수가 범주형일 때 사용합니다. 로지스틱회귀 모델은 종속변수와 독립변수 간의 관계를 로지스틱 함수로 표현합니다.

  • 그림 4-16 로지스틱 함수 시각화(출처)

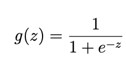
  • 그림 4-17 로지스틱 함수(출처)

그림 4-16은 로지스틱 함수의 입력값에 따른 출력값을 시각화한 그림입니다. 입력값이 음의 무한대에서 양의 무한대 까지 가지더라도 출력되는 값은 항상 0에서 1의 사이의 값을 출력합니다. 그래서 선형회귀 모델의 출력값을 로지스틱 함수의 입력값으로 주면 선형회귀 모델의 출력값이 0과 1사이의 값으로 변환됩니다. 해당 과정을 통해 범주형 변수를 예측할 수 있습니다. 최종적으로 특정 한계값(threshold)를 기준으로 두어 한계값보다 작으면 0, 한계값보다 크면 1로 예측합니다.

  • 그림 4-18 로지스틱 회귀 산식(출처)

로지스틱회귀에서는 log loss를 손실함수로 사용합니다. 개념적으로 확인해보면 실제값이 1인데 0으로 예측하면 패널티를 부가하고 실제값이 0인데 1로 예측해도 패널티를 부가하는 수식입니다.

  • 그림 4-19 log loss 산식(출처)

한 가지 재미있는점은 log loss를 손실함수로 설정한 후 경사하강법 산식을 유도해서 정리하면 선형회귀에서 사용한 경사하강법 산식과 똑같이 나옵니다.

  • 그림 4-20 로지스틱 회귀 모델의 경사하강법 산식(출처)

4.7 참고자료

4. Numpy 선형회귀 데모