선형회귀 데모¶

라이브러리 import 및 설정¶

%reload_ext autoreload
%autoreload 2
%matplotlib inline

from matplotlib import pyplot as plt
from matplotlib import rcParams
import numpy as np
from pathlib import Path
import pandas as pd
import seaborn as sns
from tqdm.notebook import tqdm
import warnings

rcParams['figure.figsize'] = (16, 8)
plt.style.use('fivethirtyeight')
pd.set_option('max_columns', 100)
pd.set_option("display.precision", 4)
warnings.simplefilter('ignore')

학습데이터 로드¶

data_dir = Path('../input/')
trn_file = data_dir / 'train.csv'
seed = 42

trn = pd.read_csv(trn_file, index_col=0)
print(trn.shape)
trn.head()

(320000, 19)

	u	g	r	i	z	redshift	dered_u	dered_g	dered_r	dered_i	dered_z	nObserve	nDetect	airmass_u	airmass_g	airmass_r	airmass_i	airmass_z	class
id
0	23.2640	20.3368	19.0095	17.6724	16.9396	-8.1086e-05	23.1243	20.2578	18.9551	17.6321	16.9089	18	18	1.1898	1.1907	1.1890	1.1894	1.1902	0
1	15.0521	14.0620	13.4524	13.2684	13.1689	4.5061e-03	14.9664	14.0045	13.4114	13.2363	13.1347	1	1	1.2533	1.2578	1.2488	1.2510	1.2555	1
2	16.7864	15.8254	15.5363	15.3935	15.3500	4.7198e-04	16.6076	15.6866	15.4400	15.3217	15.2961	2	2	1.0225	1.0241	1.0210	1.0217	1.0233	0
3	25.6606	21.1887	20.2212	19.8949	19.6346	5.8143e-06	25.3536	20.9947	20.0873	19.7947	19.5552	4	3	1.2054	1.2061	1.2049	1.2051	1.2057	0
4	24.4534	20.6992	19.0424	18.3242	17.9826	-3.3247e-05	23.7714	20.4338	18.8630	18.1903	17.8759	13	12	1.1939	1.1943	1.1937	1.1938	1.1941	0

sns.pairplot(trn.sample(n=10000), vars=['u', 'dered_u'], hue='class', size=5)

<seaborn.axisgrid.PairGrid at 0x7fda3aaba110>

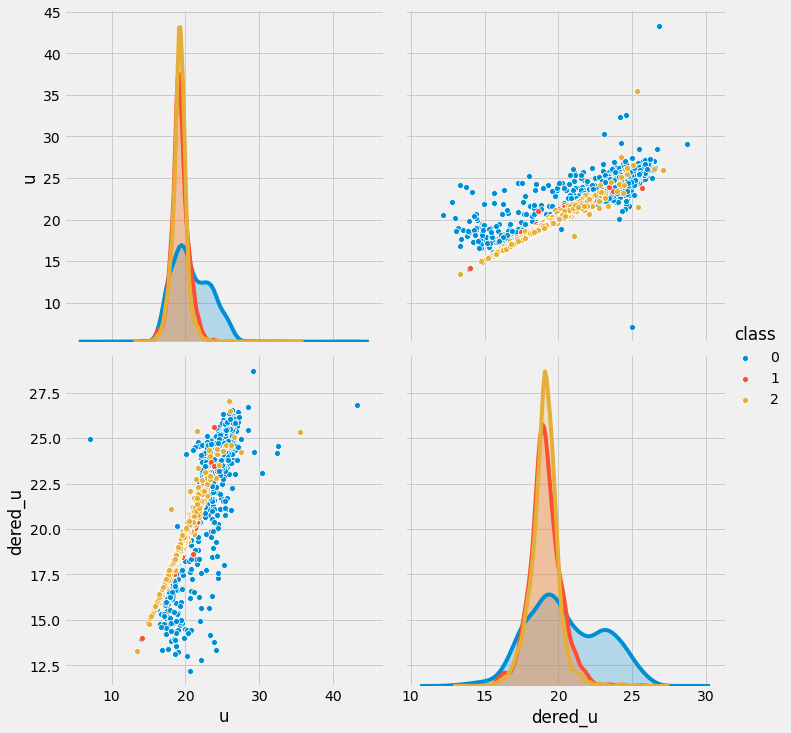
위 그래프를 통해 dered_u와 u열 간의 관계는 선형 관계를 띄고 있음을 알 수 있으며, 해당 변수들로 선형회귀 모델 구축 실습을 진행해보겠습니다.

X = trn[trn['class'] != 0][['u']].values
y = trn[trn['class'] != 0]['dered_u'].values
print(X.shape, y.shape)

(200004, 1) (200004,)

선형회귀 모델 구축 실습을 하기 위해 u열을 독립변수 X로 설정하고 dered_u열을 종속변수 y로 설정합니다. 이 때 class가 0인 샘플은 제외 합니다. 왜냐하면 시각화 그래프를 봤을 때 0인 경우는 선형관계에서 벗어나 보이므로 이번 실습에서는 0을 제외하고 class가 1 또는 2인 샘플만 사용하겠습니다.

RMSE 손실함수 정의¶

rmse = lambda y, p: np.sqrt(np.mean((y - p) ** 2))

앞서 이론을 배울 때에는 손실함수로 MSE를 배워봤습니다. 실습에서는 MSE에 루트(root)를 씌운 RMSE를 손실함수로 정의하겠습니다. RMSE는 종속변수와 스케일이 같아서 값의 의미를 해석하기 용이하기 때문에 자주 사용됩니다.

파이썬에서 함수를 정의할 때는 def()함수를 사용하기도 하지만 위의 예시처럼 lambda를 사용해서 정의할 수도 있습니다. def()로 위의 함수를 정의하면 아래와 같습니다.

def rmse(y, p):
    return np.sqrt(np.mean((y - p) ** 2))

def()를 사용하면 두 줄에 거쳐 함수를 정의하지만 lambda를 사용하면 간단한 함수인 경우 한 줄로 정의를 내릴 수 있기 때문에 유용하게 사용됩니다.

NumPy를 이용한 선형회귀¶

Numpy를 활용해 선형회귀 모델을 구축해보기 위해 필요한 정보들을 정의하겠습니다.

alpha = .001
theta0 = .1
theta1 = .1
epoch = 4

alpha는 learning rate를 뜻하며 theta0는 상수값, theta1은 X의 계수를 뜻합니다. epoch은 전체 샘플을 활용해 경사하강을 4번 실시하겠다는 의미입니다.

x = X.flatten()
print(x.shape)

(200004,)

추후 경사하강법을 적용하기 위해 zip(x, y)함수를 활용해 독립변수와 종속변수 짝을 지어줘야 하는데, zip()함수가 적용되기 위해 차원을 맞춰주는 작업입니다. X가 기존에는 2차원 array였는데 1차원으로 변경된 것을 알 수 있습니다.

rmses = []
for i in tqdm(range(epoch)):
    for x_i, y_i in zip(x, y):
        p_i =  theta0 + theta1 * x_i
        theta0 = theta0 + alpha * (y_i - p_i)
        theta1 = theta1 + alpha * (y_i - p_i) * x_i
    rmses.append(rmse(y, theta0 + theta1 * x))

위 코드는 경사하강법을 구현한 코드입니다. 먼저 p_i에 현재의 theta0와 theta1을 활용해 예측값을 구합니다. 그리고 나서 각 theta는 미분한 식에 alpha를 곱해서 업데이트를 해줍니다.

theta1, theta0

(0.9362306162023849, 1.1088813148478316)

4번의 epoch을 통해 계수가 업데이트 된 결과가 위와 같음을 알 수 있습니다.

rmses

[0.25618215910731906,
25492967552380746,
25461791287963526,
25454708923095914]

또한 손실함수인 RMSE가 epoch이 진행될 때 마다 조금씩 줄어든 것을 확인할 수 있습니다.

plt.plot(rmses)

[<matplotlib.lines.Line2D at 0x7fda3a72c790>]

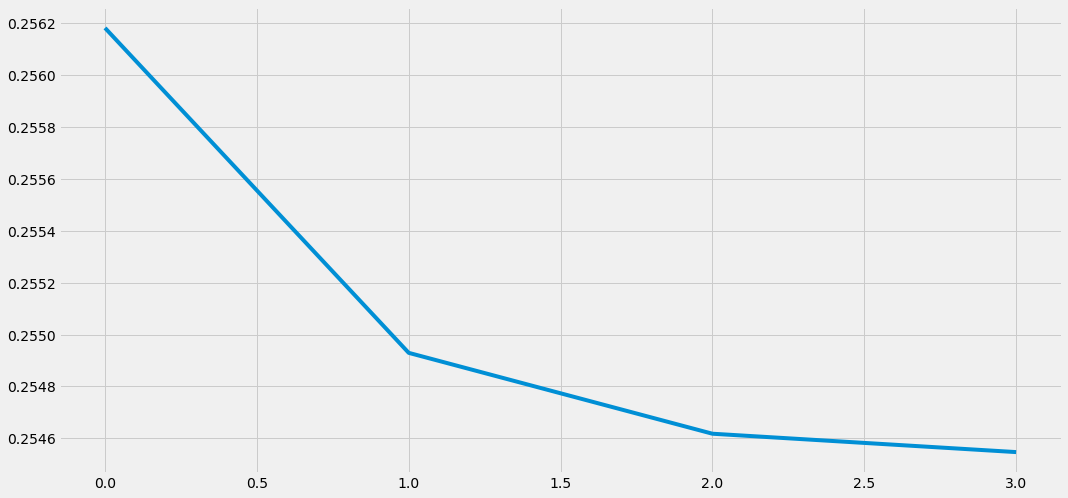
rmses를 시각화 해서 보면 위의 그래프와 같습니다. epoch진행될 수록 손실함수 값이 점점 줄어든 것을 확인할 수 있으며, 모델의 성능이 점점 좋아졌음을 알 수 있습니다.

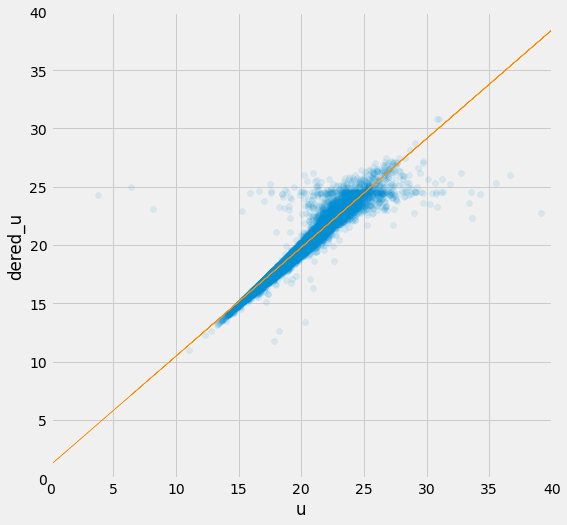
plt.figure(figsize=(8, 8))
plt.scatter(X, y, alpha=.1)
plt.plot(X, theta0 + theta1 * x, color='darkorange', linewidth=.5)
plt.xlim(0, 40)
plt.ylim(0, 40)
plt.xlabel('u')
plt.ylabel('dered_u')

Text(0, 0.5, 'dered_u')

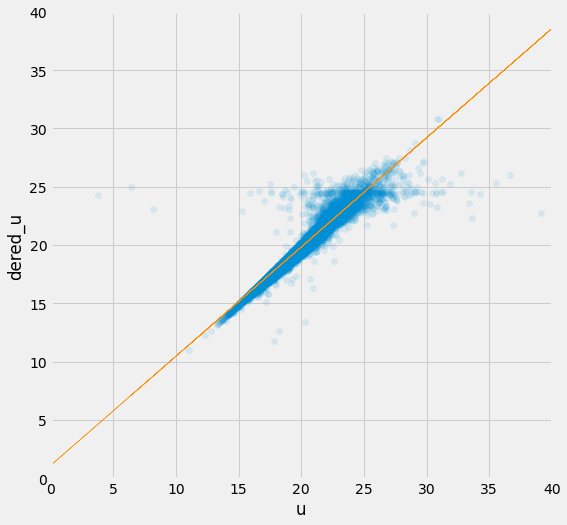
실제값과 모델의 예측값을 그래프로 그려보면 위와 같습니다. 파란 점들은 실제값을 나타내며 주황색 선은 경사하강법을 통해 학습한 선형회귀 모델이 예측한 값입니다. 꽤 정확하게 예측하고 있음을 확인할 수 있습니다.

scikit-learn을 이용한 선형회귀¶

실제 분석을 할 시에는 numpy로 경사하강법을 직접 구현할 필요는 없습니다. scikit-learn 라이브러리에서 제공하는 함수를 활용해 2~3줄만에 쉽게 선형회귀 모델을 구축할 수 있기 때문입니다.

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(X, y)
p = lr.predict(X)

sklearn.linear_model 모듈 내에 있는 LinearRegression함수를 가지고와서 lr변수에 선형회귀 모델 객체를 생성해준 후 fit()명령어에 독립변수와 종속변수를 입력해서 선형회귀 모델을 학습시켜 줍니다. 그리고 predict()함수를 통해 예측을 해서 예측값을 p변수에 저장해줍니다.

rmse(y, p)

0.2522450693360897

예측한값과 실제값과의 rmse가 0.2522가 나온것을 확인할 수 있습니다. numpy로 직접구현해서 4번의 epoch동안 경사하강법을 적용했을 때는 rmse가 0.2545가 나왔는데, scikit-learn으로 학습을 하니 단번에 rmse가 더 줄어든 것을 확인할 수 있습니다.

lr.coef_, lr.intercept_

(array([0.9320425]), 1.1556424178625342)

lr.coef_와 lr.intercept_를 사용해 학습된 계수를 확인해보니 numpy로 학습했을 때의 계수와 유사한 것을 확인할 수 있습니다.

plt.figure(figsize=(8, 8))
plt.scatter(X, y, alpha=.1)
plt.plot(X, p, color='darkorange', linewidth=.5)
plt.xlim(0, 40)
plt.ylim(0, 40)
plt.xlabel('u')
plt.ylabel('dered_u')

Text(0, 0.5, 'dered_u')

마찬가지로 위의 그래프는 scikit-learn으로 학습한 선형회귀 모델의 예측값이 주황색으로 표시된 그래프입니다.

scikit-learn을 이용한 로지스틱회귀¶

X = trn[trn['class'] != 0].drop('class', axis=1)
y = trn[trn['class'] != 0]['class'].values - 1

scikit-learn을 활용해 로지스틱회귀 모델을 구축하기 위해 간단한 데이터 처리를 먼저 진행하겠습니다. 현재 class에는 3개의 범주 (0, 1, 2)가 존재합니다. 이번 실습에서는 간단한 이진 분류 문제로 변형하기 위해 0인 class를 제외한 데이터만으로 실습을 진행해보겠습니다.

class를 제외한 모든 변수를 독립변수 X에 저장하고 class는 종속변수 y에 저장합니다. 0을 제외하면 class에는 1과 2가 남게 됨으로 y변수에는 1과 2만 존재합니다. 해당 범주를 0과 1로 변형하기 위해서 1을 빼줍니다.

np.unique(y)

array([0, 1])

1을 빼줘서 class를 0과 1로 만들어 주었기 때문에 y에 존재하는 고윳값을 np.unique()함수를 통해 확인해보면 0과 1만 있음을 알 수 있습니다.

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import log_loss, roc_auc_score

lr = LogisticRegression()
lr.fit(X, y)
p = lr.predict_proba(X)[:, 1]

sklearn.linear_model 모듈에서 LogisticRegression함수를 불러오고 sklearn.metrics에서 log_loss와 roc_auc_score함수를 불러옵니다. log_loss는 로지스틱회귀를 학습/평가할 때 사용하는 손실함수이며 roc_auc_score는 분류 모델의 성능을 측정할 때 사용하는 대표적인 지표입니다.

로지스틱회귀 모델을 학습하기 위해 LogisticRegression()객체를 lr변수에 저장하고 fit()함수에 독립변수와 종속변수를 입력해 모델을 학습합니다.

범주형 모델로 예측을 수행하기 위해선 predict() 또는 predict_proba()를 사용할 수 있습니다. predict()함수는 0 또는 1의 범주를 반환하며 predict_proba()는 각 범주에 속할 확률을 반환니다. proba는 probability(확률)의 약자입니다.

predict_proba()실행하면 n행 2열로 된 2차원의 배열이 반환됩니다. n은 입력값 X의 행의 개수와 같으며 열이 2개인 경우는 이번 실습에서 사용한 범주의 개수가 2개이기 때문입니다. 첫번째 열은 범주 0에 속할 확률이며 두번째 열은 범주 1에 속할 확률이 저장돼있습니다. 그 중 두번째 열에 있는 확률 값을 선택해 p변수에 저장합니다.

lr.coef_, lr.intercept_

(array([[ 0.81266917,  0.08317138, -1.87245322,  0.51565384, -0.54844623,
         -1.58805578,  2.26069235, -0.05486364, -1.36138002,  0.57936571,
         -0.59896011,  0.08585678, -0.10280546, -0.14195166, -0.1445912 ,
         -0.13945722, -0.14068748, -0.14325409]]),
 array([0.22177582]))

로지스틱 회귀 모델의 학습된 계수를 위의 명령어를 통해 확인할 수 있습니다.

log_loss(y, p)

0.3656496250562368

roc_auc_score(y, p)

0.8761459752003657

from kaggler.metrics import plot_roc_curve, plot_pr_curve

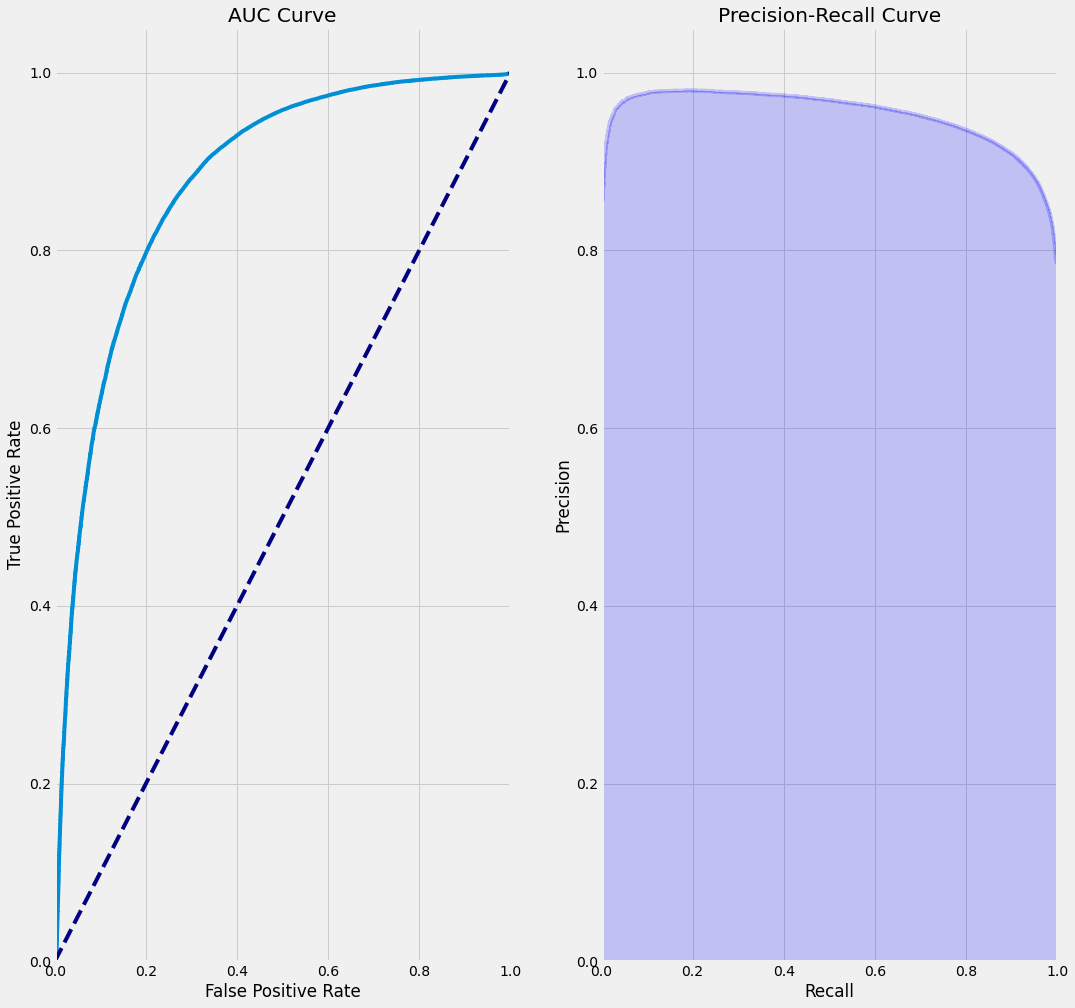
아래는 kaggler라이브러리에서 제공하는 함수를 활용해 auc curve와 precision-recall curve를 그리는 과정입니다. 해당 그래프는 분류모델의 성능을 평가시 자주 사용하는 그래프입니다.

plt.figure(figsize=(16, 16))
plt.subplot(1, 2, 1)
plot_roc_curve(y, p);
plt.title('AUC Curve')
plt.subplot(1, 2, 2)
plot_pr_curve(y, p);
plt.title('Precision-Recall Curve')

Text(0.5, 1.0, 'Precision-Recall Curve')

단국대 2020 캐글 뽀개기